Teorema reprezintă o afirmație al cărei adevăr se stabilește prin demonstrație.
Fiecare ramură a matematicii este constituită dintr-un șir de teoreme, demonstrația fiecăreia dintre ele sprijinindu-se pe teorema care o precedă.
TEOREMA LUI PITAGORA
Teorema lui Pitagora este una dintre cele mai cunoscute teoreme din geometria euclidiană, constituind o relație între cele trei laturi ale unui triunghi dreptunghic.
Teorema lui Pitagora afirmă că în orice triunghi dreptunghic, suma pătratelor catetelor este egală cu pătratul ipotenuzei (latura opusă unghiului drept).
Teorema poate fi scrisă sub forma unei relații între cele trei laturi a, b șic, câteodată denumită relația lui Pitagora.
unde c reprezinta lungimea ipotenuzei, iar a si
b lungimile celorlalte doua laturi ale triunghiului.
TEOREMA LUI THALES
Thales din Milet (624-546 i. Hr.), dupa cum afirma Proclus, ar fi cunoscut teoremele privitoare la triunghiurile asemenea, cu ajutorul carora a masurat departarea unui vas de la tarmul marii.
De asemenea, tot cu ajutorul unor teoreme de geometrie, el ar fi masurat inaltimea marei piramide a lui Keops. Astazi, sub numele de "teorema lui Thales" sunt cunoscute legaturile care exista intr-o configuratie de cinci pucte, ABCDE, unde A, B, D sunt coliniare, A, C, E sunt coliniare, iar DE este paralela cu BC.
De aici de pot
lamuri mai departe asemanarea a doua triunghiuri (sase puncte) si mai departe,
asemanarea a doua figuri geometrice in spatiul tridimensional sau cu mai multe
dimensiuni. Se poate caracteriza o geometrie prin atributul
"thalesiana", indicand ca in acea geomtrie functioneaza teorema lui
Thales.
De aici de pot
lamuri mai departe asemanarea a doua triunghiuri (sase puncte) si mai departe,
asemanarea a doua figuri geometrice in spatiul tridimensional sau cu mai multe
dimensiuni. Se poate caracteriza o geometrie prin atributul
"thalesiana", indicand ca in acea geomtrie functioneaza teorema lui
Thales.



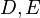








0 comments:
Post a Comment